MD5信息摘要算法
MD5
MD5的全称是Message-Digest Algorithm,是Hash算法中的一种重要算法,具有单项加密、加密结果唯一、安全性能好等特点。MD5以512位分组来处理输入的信息 ,且每一分组又被划分为16个 32位子分组,经过了一系列的处理后 ,算法的输出由四个32位分组组成,将这四个32位分组级联后将生成一个128位散列值。
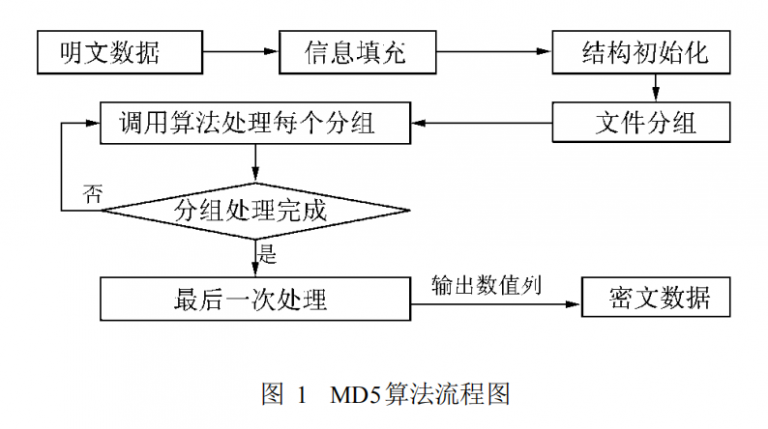
MD5特点
压缩性: 任意长度的数据,算出的MD5值长度都是固定的。 容易计算: 从原数据计算出MD5值很容易。 抗修改性: 对原数据进行任何改动,哪怕只修改1个字节,所得到的MD5值都有很大区别。 强抗碰撞: 已知原数据和其MD5值,想找到一个具有相同MD5值的数据(即伪造数据)是非常困难的。
信息填充
- 首先需要对明文信息进行填充,使其位长度对512求余的结果等于448。因此,信息的位长度(Bits Length)将被扩展至 N*512 + 448。
- 然后,再在这个结果后面附加一个以64位二进制表示的填充前信息长度。
- 经过这两步的处理 ,现在的信息字节长度为 N512 + 448 + 64 = (N + 1) 512,即长度恰好是 512的整数倍。
结构初始化
在处理过程中需要定义一个结构。该结构包含了每一次需要处理的一个明文块 (512bit)和计算出来的散列值 (128bit)。在散列的整个过程中,它的作用非常重要 ,各个明文块计算出来的散列值都是通过它来传递的。
处理分组,循环加工
ABCD都是32位,分别与真实数据的每32位做运算
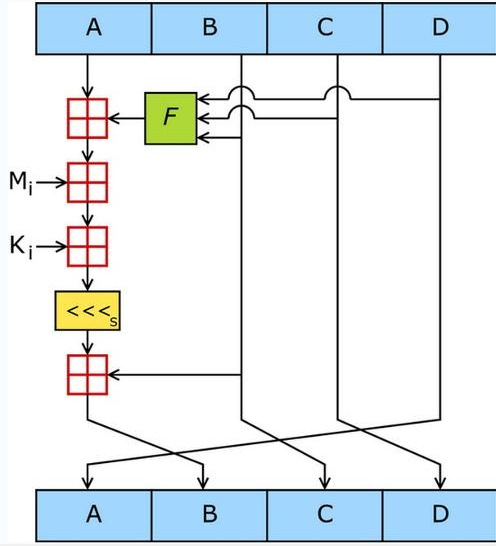
图中,A,B,C,D就是哈希值的四个分组。每一次循环都会让旧的ABCD产生新的ABCD。一共进行多少次循环呢?由处理后的原文长度决定。 假设处理后的原文长度是M 主循环次数 = M / 512 每个主循环中包含 512 / 32 * 4 = 64 次 子循环。
绿色F
绿色F,代表非线性函数。官方MD5所用到的函数有四种:
F(X, Y, Z) =(X&Y) | ((~X) & Z)
G(X, Y, Z) =(X&Z) | (Y & (~Z))
H(X, Y, Z) =X^Y^Z
I(X, Y, Z)=Y^(X|(~Z))
在主循环下面64次子循环中,F、G、H、I 交替使用,第一个16次使用F,第二个16次使用G,第三个16次使用H,第四个16次使用I。
红色“田”字
很简单,红色的田字代表相加的意思。
Mi
Mi是第一步处理后的原文。在第一步中,处理后原文的长度是512的整数倍。把原文的每512位再分成16等份,命名为M0~M15,每一等份长度32。在64次子循环中,每16次循环,都会交替用到M1~M16之一。
Ki
一个常量,在64次子循环中,每一次用到的常量都是不同的。
黄色的<<
主循环有M / 512轮,每轮循环都很相似。第一轮进行16次操作。每次操作对 a、b、c和 d中的其中三个作一次非线性函数运算 ,然后将所得结果加上第四个变量,一个子分组和一个常数。再将所得结果向右环移一个不定的数,并加上 a、b、c或 d中之一,最后用该结果取代 a、b、c或 d中之一。
FF(a,b,c,d,Mj,s,ti)表示a=b+((a+F(b,c,d)+Mj+ti)<<<s)
GG(a,b,c,d,Mj,s,ti)表示a=b+((a+G(b,c,d)+Mj+ti)<<<s)
HH(a,b,c,d,Mj,s,ti)表示a=b+((a+H(b,c,d)+Mj+ti)<<<s)
II(a,b,c,d,Mj,s,ti)表示a=b+((a+I(b,c,d)+Mj+ti)<<<s)
第一轮
a=FF(a,b,c,d,M0,7,0xd76aa478)
b=FF(d,a,b,c,M1,12,0xe8c7b756)
c=FF(c,d,a,b,M2,17,0x242070db)
d=FF(b,c,d,a,M3,22,0xc1bdceee)
a=FF(a,b,c,d,M4,7,0xf57c0faf)
b=FF(d,a,b,c,M5,12,0x4787c62a)
c=FF(c,d,a,b,M6,17,0xa8304613)
d=FF(b,c,d,a,M7,22,0xfd469501)
a=FF(a,b,c,d,M8,7,0x698098d8)
b=FF(d,a,b,c,M9,12,0x8b44f7af)
c=FF(c,d,a,b,M10,17,0xffff5bb1)
d=FF(b,c,d,a,M11,22,0x895cd7be)
a=FF(a,b,c,d,M12,7,0x6b901122)
b=FF(d,a,b,c,M13,12,0xfd987193)
c=FF(c,d,a,b,M14,17,0xa679438e)
d=FF(b,c,d,a,M15,22,0x49b40821)
第二轮
a=GG(a,b,c,d,M1,5,0xf61e2562)
b=GG(d,a,b,c,M6,9,0xc040b340)
c=GG(c,d,a,b,M11,14,0x265e5a51)
d=GG(b,c,d,a,M0,20,0xe9b6c7aa)
a=GG(a,b,c,d,M5,5,0xd62f105d)
b=GG(d,a,b,c,M10,9,0x02441453)
c=GG(c,d,a,b,M15,14,0xd8a1e681)
d=GG(b,c,d,a,M4,20,0xe7d3fbc8)
a=GG(a,b,c,d,M9,5,0x21e1cde6)
b=GG(d,a,b,c,M14,9,0xc33707d6)
c=GG(c,d,a,b,M3,14,0xf4d50d87)
d=GG(b,c,d,a,M8,20,0x455a14ed)
a=GG(a,b,c,d,M13,5,0xa9e3e905)
b=GG(d,a,b,c,M2,9,0xfcefa3f8)
c=GG(c,d,a,b,M7,14,0x676f02d9)
d=GG(b,c,d,a,M12,20,0x8d2a4c8a)
第三轮
a=HH(a,b,c,d,M5,4,0xfffa3942)
b=HH(d,a,b,c,M8,11,0x8771f681)
c=HH(c,d,a,b,M11,16,0x6d9d6122)
d=HH(b,c,d,a,M14,23,0xfde5380c)
a=HH(a,b,c,d,M1,4,0xa4beea44)
b=HH(d,a,b,c,M4,11,0x4bdecfa9)
c=HH(c,d,a,b,M7,16,0xf6bb4b60)
d=HH(b,c,d,a,M10,23,0xbebfbc70)
a=HH(a,b,c,d,M13,4,0x289b7ec6)
b=HH(d,a,b,c,M0,11,0xeaa127fa)
c=HH(c,d,a,b,M3,16,0xd4ef3085)
d=HH(b,c,d,a,M6,23,0x04881d05)
a=HH(a,b,c,d,M9,4,0xd9d4d039)
b=HH(d,a,b,c,M12,11,0xe6db99e5)
c=HH(c,d,a,b,M15,16,0x1fa27cf8)
d=HH(b,c,d,a,M2,23,0xc4ac5665)
第四轮
a=II(a,b,c,d,M0,6,0xf4292244)
b=II(d,a,b,c,M7,10,0x432aff97)
c=II(c,d,a,b,M14,15,0xab9423a7)
d=II(b,c,d,a,M5,21,0xfc93a039)
a=II(a,b,c,d,M12,6,0x655b59c3)
b=II(d,a,b,c,M3,10,0x8f0ccc92)
c=II(c,d,a,b,M10,15,0xffeff47d)
d=II(b,c,d,a,M1,21,0x85845dd1)
a=II(a,b,c,d,M8,6,0x6fa87e4f)
b=II(d,a,b,c,M15,10,0xfe2ce6e0)
c=II(c,d,a,b,M6,15,0xa3014314)
d=II(b,c,d,a,M13,21,0x4e0811a1)
a=II(a,b,c,d,M4,6,0xf7537e82)
b=II(d,a,b,c,M11,10,0xbd3af235)
c=II(c,d,a,b,M2,15,0x2ad7d2bb)
d=II(b,c,d,a,M9,21,0xeb86d391)
每轮循环后,将A,B,C,D分别加上a,b,c,d,然后进入下一循环.
输出结果
当全部信息处理完成后 ,将分组处理的结果进行处理,输出计算结果。
所有这些完成之后 ,将 A、B、C、D分别加上 a、b、c、d。然后用下一分组数据继续运行算法 ,最后的输出是 A、B、C和 D的级联。当全部分组处理完成后,将结果级联 ,即得到了 MD5处理的结果。
MD5算法原理--用途
1、防止被篡改,比如我提供文件下载,为了防止不法分子在安装程序中添加木马,我可以在网站上公布由安装文件得到的MD5输出结果。
2、防止直接看到明文,现在很多网站在数据库存储用户的密码的时候都是存储用户密码的MD5值。这样就算不法分子得到数据库的用户密码的MD5值,也无法知道用户的密码。
3、防止抵赖(数字签名),例如A写了一个文件,认证机构对此文件用MD5算法产生摘要信息并做好记录。这样可以防止出现以后A不承认此事而带来的麻烦。
解释问题
MD5为什么能把一个不管多长的文件都变成定长的?
MD5使用4个32位的数据,和数据中的每个32位的数据进行计算,最终输出这4个32位数
MD5为什么是不可逆的
//如果一个函数入参只有一个X那么告诉你Z的结果很容易推导出X
F(X) = Z
X*3 = Z
//但是如果入参是多个,比如X,Y,那么就算很简单的加法函数,
//你也没法直接通过Z推导出X、Y只能枚举。何况MD5这么多入参
F(X,Y) = Z
X+Y = Z
MD5到底会不会重复,概率有多大
MD5是个128位的数,那么假设有N个完全不同的文件足够随机足够散列 那么当N大于2^128时才有可能出现重复
2^128 -> 10^32 -> 10^8*10^24 -> 中一百万亿亿次头等大奖的彩票
MD5算法可以破解么?为什么?网上有在线破解是怎么回事?
参考https://blog.csdn.net/dawn_after_dark/article/details/54429766
答:MD5算法不可以破解。
因为MD5是单向散列函数,输入任意长度的信息,经过处理,输出为128位的信息;不同的输入得到的不同的结果;根据128位的输出结果不可能反推出输入的信息。所以不能从密文(散列值)反过来得到原文,即没有解密算法。
MD5计算的过程中丢失了信息,一个MD5的值可以对应多个原文。一个MD5理论上的确是可能对应无数多个原文的,因为MD5是有限多个的而原文可以是无数多个。比如主流使用的MD5将任意长度的“字节串映射为一个128bit的大整数。也就是一共有2^128种可能,大概是3.4*10^38,这个数字是有限多个的,而但是世界上可以被用来加密的原文则会有无数的可能性。
举个简单例子:
原文:我今年大四
加密规则:
每个字取拼音声调+笔画数,最后的结果计算乘积,为了也使得我的结果始终保持在一个限定范围内,取最后结果取其与2^14=16384的余数,如“我”是7画3声,也就是“特征值10”,以此类推,今4+1=5 年5+2=7 大3+4=7 四5+4=9,最后我发明的不可逆函数值就是105779=22050与16384的余数,也就是5666,如果单单给5666这个数字和加密算法,无论如何不可能推出原文是“我今年大四”的,不过如果给你“我今年大四”你却很容易验证答案是否正确。
网上有在线破解:
网上md5的破解主要都是采用暴力生成各种字符串组合然后进行hash,很多用户的密码都不够复杂,所以很容易被这种方式生成出来。防范这种方式的办法一个是随机salt,只要salt够随机也够长,就会带来巨大的状态空间,极大降低被暴力生成到的可能。另一个办法是生成hash的速度够慢,比如迭代1000次,这样就大大降低了暴力运算的速度。
还有种破解就是采用彩虹表和字典:通过数据库把常见字符转的MD5存储起来为彩虹表,然后直接反查。有两种方法得到字典,一种是日常搜集的用做密码的字符串表,另一种是用排列组合方法生成的,先用MD5程序计算出这些字典项的MD5值,然后再用目标的MD5值在这个字典中检索。
比如我通过大量例子发现某密文中A对应C,然后我会记在数据字典中,下次直接用C代替A,看上去好像了破解了,实则并没有破解,只是找到了规律适应这种密文而已。